Paper Review: Understanding Deep Learning Requires Rethinking Generalization
500 words essay for Google AI Summer School. 🚀
Table of contents
Introduction
The paper “Understanding Deep Learning Requires Rethinking Generalization” [1] caused quite a stir in the Deep Learning and Machine Learning research communities, and was one of the three papers awarded the Best Paper Award in ICLR 2017. This paper approaches the question:
"What is it that distinguishes neural networks that generalize well from those that don’t?"
It tries to mitigate some of the existing misconceptions in that regard, through a host of randomization tests and touches upon how generalization error may or may not be related to regularization and loss. It also throws light on some interesting points like the finite-sample expressivity of neural nets and how solving the gram matrix in SGD gives us the minimum l2 norm but is not predictive of minimal generalization error. Let’s look at these findings in a bit more detail.
Findings
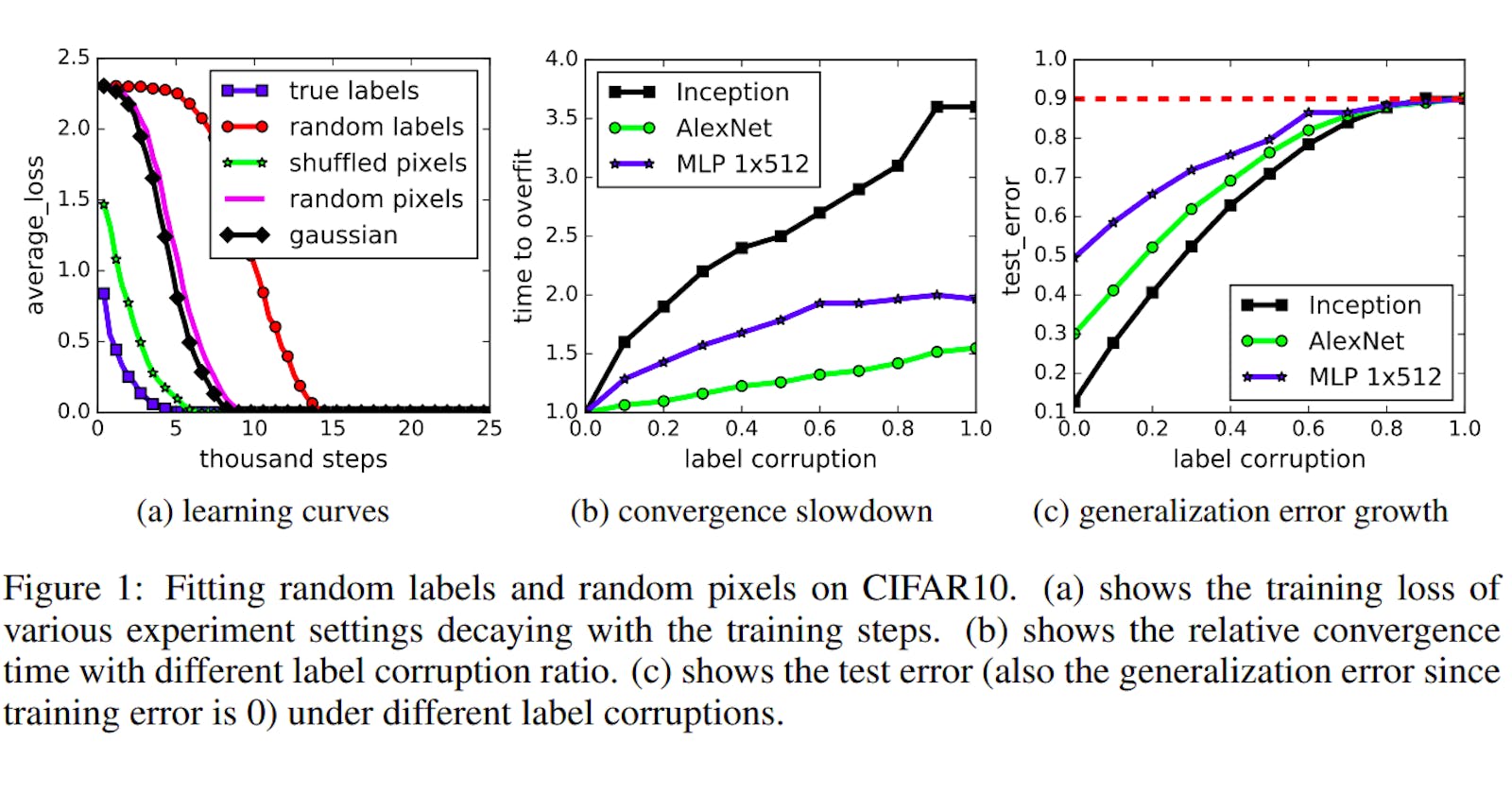
The most intriguing and unique strategy adopted by the researchers is randomization testing, wherein they train neural networks with true labels, partially corrupted labels (some labels are random labels from uniform distribution), completely random labels from uniform distribution and shuffled pixels, firstly, all having the same shuffling pattern and then with random pixels shuffling, and even from Gaussian noise samplings from original dataset. It is obvious that any correlation, meaningful to humans, between the image and the label is gradually broken. Despite this, the authors find that even from complete noise the neural network correctly ‘shatters’ the training data, ie. fit to training data with 100% accuracy, with same network structure and hyperparameters!
It is thus proved deep neural networks can easily fit random labels. The effective capacity of neural nets is sufficient for memorizing the entire data set, given enough parameters and optimization on random labels remains easy ie. it increases by a reasonably small constant factor, refuting some of the findings from the paper titled “Deep Nets don’t learn via memorization” by Krueger et al from the same conference. It’s not a complete paradox though as the researchers from the two papers have found some similar results but drawn different conclusions, observing them in different lights.
For eg, both research groups observed that with increase in noise, networks take a bit longer to shatter training data. On one hand, Krueger et al. concluded that Neural nets did not memorize the data, and captured patterns only. On the contrary, Zhang et al concluded that since the time taken was more by just a small factor, they might really be memorizing the training data, additionally they note that gaussian noise converged faster than random labels, corroborating their hypothesis. Finally, they note that generalization error is certainly dependent on the network choice, as observed, Inception gave the least generalization error against AlexNet and a 512x MLP.
The paper discusses the effectiveness of some regularization techniques:.
Augmenting data shows better generalization performance than weight decay, biggest gains are achieved by changing the model architecture.
Early stopping could improve generalization, but that is not always true. Batch normalization improves generalization.
The authors write, "Explicit regularization may improve generalization but is neither necessary nor by itself sufficient.”
Universal Function Approximation Theorem states that a single hidden layer, containing a finite number of neurons, can approximate any continuous function on compact subsets of Euclidean space, but does not comment on the algorithmic learnability of those parameters, ie. how feasibly or quickly this neural net will actually learn these weights. This is extended to their theorem when they say, “Given a particular set of data or fixed population level n in d dimensions, there exists a two-layer neural network with ReLU activations and 2n+d weights that can represent any function.”
Conclusion
The main findings of the paper can be concluded as, “Both explicit and implicit regularizers could help to improve the generalization performance. However, it is unlikely that the regularizers are the fundamental reason for generalization.”
This paper has a lot of interesting results, though it couldn’t offer effective solutions to some problems. I find it to be as groundbreakingly exciting as say the AlexNet paper in 2012, or the Dropout paper in 2014 (references below), which enlightened us with profound insights into neural networks.